Una ecuación de segundo grado o ecuación cuadrática, es aquella en la cual la mayor potencia de la incógnita considerada en la ecuación, es dos. La expresión general de una ecuación cuadrática es

donde x representa la variable y a, b y c son constantes; a es un coeficiente cuadrático (distinto de 0), b el coeficiente lineal y c es el término independiente.
La gráfica de una función cuadrática es una parábola. La ecuación cuadrática proporciona las intersecciones de la parábola con el eje de las abscisas, que pueden ser en dos puntos, en uno o ninguno.
El origen y la solución de las ecuaciones de segundo grado son de gran antigüedad. En Babilonia se conocieron algoritmos para resolverla.
En Europa: a) en Grecia las desarrolló el matemático Diofanto de Alejandría; b) el matemático judeoespañol Abraham bar Hiyya, en suLiber embadorum, introdujo la solución de estas ecuaciones.
De una ecuación cuadrática con coeficientes reales o complejos existen siempre dos soluciones, no necesariamente distintas, llamadas raíces, que pueden ser reales o complejas. Se denomina fórmula cuadrática3 a la ecuación que proporciona las raíces de la ecuación cuadrática:
 ,
,
donde el símbolo ± indica que los valores
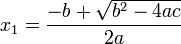
y 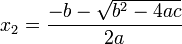


No hay comentarios:
Publicar un comentario